일반적으로 무게중심이라고 하면, COG(Center of Gravity) or COM(Center of Mass)를 말한다.
그리고, 로봇의 무게중심에 작용하는 모든 모멘트의 합이 0이 되는 지점을 ZMP(Zero Moment Point)라고 한다.
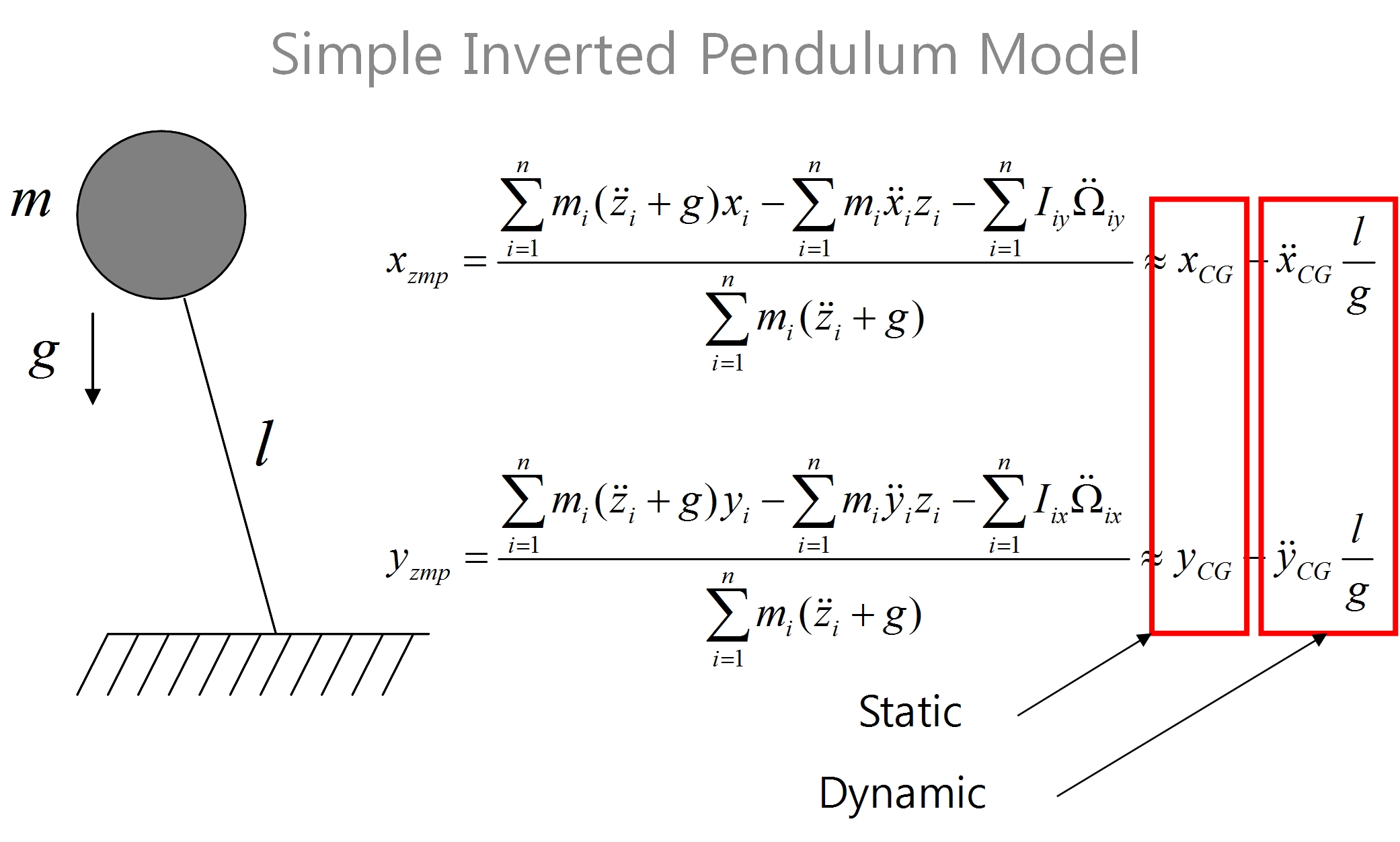
위 모델은 로봇의 모든 무게중심을 단일질량모델로 봤을때, 즉 위의 m은 로봇의 모든 질량의 중심을 말하고,
g는 중력가속도, l은 지면부터 그 무게중심까지의 거리를 의미한다.
위에 있는 식은 일반적인 zmp식이다. kaist의 휴보나 여타 해외의 휴머노이드 로봇들은 위의 zmp수식을 사용한다. 많이 일반화 되어있는 폼이다. zmp수식에서 i는 링크의 축번호인데, 로봇의 단일질량모델로 모델링 하였을경우 링크는 1개가 되는, simple inverted pendulum모델이 될것이다.
수식의 각 요소를 보면, m은 질량, g는 중력가속도, I는 관성모멘트, Ω은 각도인데 2dot은 각가속도 이다.
x,y,z는 무게중심의 좌표이고 2dot이면 x,y,z에 대한 선가속도가 될것이다.
운동은 직선운동과 회전운동으로 분리될 수 있는데, zmp식에서도 무게중심의 직선운동에 대한것과 회전운동에 대한 항이 포함되어 있다. 즉, 무게중심의 x,y,z축별 운동과 지면에 대한 회전운동이다.
zmp식을통해 로봇의 모션에 대한 zmp를 계산할 수 있고, 이것으로 로봇의 보행또는 이동시 안정도(stability index)를 얻을 수 있게된다.
그리고, 계산 퍼포먼스측면이나 식의 단순화를 위해 우측의 붉은색으로 표시된 식을 사용하기도 한다.
위와같이 x,y에 대한 zmp를 직접 계산할 수도 있지만, 오른쪽식처럼 근사값을 이용할 수도있다.
식의 의미는 동일해 보인다. X,Y 각 축의 Center of Gravity에 대한 위치와 질량을 각 축에 대한 선가속도성분이 길이와 중력가속도에 의해 변화되는것을 보면...(자세한 식의 유도는 따로 정리를 해야겠다.)
따라서, 일반적으로 위의 식으로 계산된 결과가 desired zmp 또는 calculated zmp로 실제 센서에 의해 측정된 zmp와 비교되어 desired zmp를 추종하는 제어기를 설계할 수 있는 기반을 마련하는 것이다.
'Robotics > Control Tech.' 카테고리의 다른 글
| 강체운동과 동차변환(Rigid Motions and Homogeneous Transformations) (0) | 2008.11.05 |
|---|---|
| 로봇동역학을 위한 기본개념 (2) | 2008.11.05 |
| 보간법(Interpolation) (0) | 2008.06.15 |
| 자코비안(jacobian) (8) | 2008.06.02 |
| 휴머노이드 HRP 관련 논문 모음 (2) | 2008.05.27 |
